large-anon: Practical scalable anonymous records for Haskell

The large-anon library provides support for anonymous records; that is, records that do not have to be declared up-front. For example, used as a plugin along with the record-dot-preprocessor plugin, it makes it possible to write code such as this:

magenta :: Record [ "red" := Double, "green" := Double, "blue" := Double ]
magenta = ANON { red = 1, green = 0, blue = 1 }

reduceRed :: RowHasField "red" r Double => Record r -> Record r
reduceRed c = c{red = c.red * 0.9}

The type signatures are not necessary; type inference works as aspected for these records. If you prefer to use lenses¹, that is also possible:

reduceBlue :: RowHasField "blue" r Double => Record r -> Record r
reduceBlue = over #blue (* 0.9)

The library offers a small but very expressive API, and it scales to large records (with 100 fields and beyond), with excellent compilation time performance and good runtime performance. In this blog post we will first present the library from a user’s perspective, then give an overview of the internals with an aim to better to understand the library’s runtime characteristics, and finally show some benchmarks. The library is available from Hackage and is currently compatible with ghc 8.8, 8.10 and 9.0 (extending this to 9.2 should not be too hard).

If you want to follow along, the full source code for all the examples in this blog post can be found in Test.Sanity.BlogPost in the large-anon test suite.

The simple interface

The library offers two interfaces, “simple” and “advanced”. We will present the simple interface first, then explore the advanced interface below.

The simple interface can be summarized as follows:

Data.Record.Anon.Simple

data Record (r :: Row Type)
  deriving (Eq, Ord, Show, Large.Generic, ToJSON, FromJSON)

data Pair a b = a := b
type Row k = [Pair Symbol k]

instance (RowHasField n r a, ..) => HasField n (Record r) a

empty   :: Record '[]
insert  :: Field n -> a -> Record r -> Record (n := a : r)
get     :: RowHasField n r a => Field n -> Record r -> a
set     :: RowHasField n r a => Field n -> a -> Record r -> Record r
project :: SubRow r r' => Record r -> Record r'
inject  :: SubRow r r' => Record r' -> Record r -> Record r
merge   :: Record r -> Record r' -> Record (Merge r r')

where Large.Generic comes from the large-generics package.

In the remainder of this section we will introduce this API by means of examples. When there is possibility for confusion, we will use the prefix S. to refer to the simple interface (and A. for the advanced interface).

Record construction and field access

In the introduction we used some syntactic sugar: the ANON record constructor makes it possible to use regular record syntax for anonymous records. This syntax is available as soon as you use the large-anon plugin. ANON desugars to calls to empty and insert; it does not depend on any kind of internal or unsafe API) and there is no need to use it if you prefer not to (though see Applying pending changes):

purple :: Record [ "red" := Double, "green" := Double, "blue" := Double ]
purple =
     S.insert #red   0.5
   $ S.insert #green 0
   $ S.insert #blue  0.5
   $ S.empty

Similarly, the example in the introduction used RecordDotSyntax as provided by record-dot-preprocessor, but we can also use get and set:

reduceGreen :: RowHasField "green" r Double => Record r -> Record r
reduceGreen c = S.set #green (S.get #green c * 0.9) c

Constraints

The summary of the simple interface showed that Record has a Show instance. Let’s take a closer look at its precise signature:

instance (KnownFields r, AllFields r Show) => Show (Record r)

The KnownFields constraint says that the field names of r must be known, and the AllFields r Show constraint says that all fields of r must in turn satisfy Show; the show instance uses this to output records like this:

> magenta
ANON {red = 1.0, green = 0.0, blue = 1.0}

In fact, Show for Record simply uses gshow from large-generics.

The order of the fields is preserved in the output: large-anon regards records with rows that differ only in their order as different types; isomorphic, but different. The project function can be used to translate between records with different field order; we shall see an example when we discuss sequenceA.

The RowHasField, KnownFields, AllFields and SubRow constraints (for project) are solved by the large-anon typechecker plugin, so you will need to add

{-# OPTIONS_GHC -fplugin=Data.Record.Anon.Plugin #-}

at the top of your Haskell file. We will see later how to manually prove such constraints when the plugin cannot.

Project and inject

In the previous section we saw that project can be used to reorder fields, but is actually more general than that. In addition to reordering fields, we can also omit fields: a SubRow r r' constraint is satisfied whenever the fields of r' are a subset of the fields of r. Moreover, when SubRow r r' holds we can also update the larger record from the smaller one: project and inject together form a lens.

Let’s consider an example. Suppose we have some kind of renderer with a bunch of configuration options:

type Config = [
      "margin"   := Double
    , "fontSize" := Int
    , "header"   := String
    , ...
    ]

defaultConfig :: Record Config
defaultConfig = ANON {
      margin   = 1
    , fontSize = 18
    , header   = ""
    , ...
    }

render :: Record Config -> ...

To call render, we would need to construct such a record; for example, we could do²

render $ defaultConfig{margin = 2}

There is an alternative, however. Rather than passing in the full configuration, we could offer an API where the caller only passes in the overrides:

render' :: SubRow Config overrides => Record overrides -> ...
render' overrides = render (S.inject overrides defaultConfig)

Now we no longer need to export a defaultConfig to the user:

render' $ ANON { margin = 2 }

The advanced interface

The key difference between the simple interface and the advanced one is that Record is additionally parameterised by a type constructor f:³

data Record (f :: k -> Type) (r :: Row k)

Intuitively, every field in the record will be wrapped in an application of f. Indeed, the simple interface is but a thin layer around the advanced one, instantiating f to the identity functor I:

magenta' :: A.Record I [ "red" := Double, "green" := Double, "blue" := Double ]
magenta' = S.toAdvanced magenta

The additional type constructor argument makes records a lot more expressive, and consequently the advanced API is much richer than the simple one. We will give some representative examples.

Foldable and zipping

“Folding” (as in Foldable) essentially means “turning into a list”. With records we cannot do that, unless all fields of the record happen to have the same type. We can express this by using the constant functor K:

collapse :: Record (K a) r -> [a]
toList   :: KnownFields r => Record (K a) r -> [(String, a)]

Similarly, because every field in the record has a different type, zipping requires a polymorphic function:

zipWith :: (forall x. f x -> g x -> h x) -> Record f r -> Record g r -> Record h r

(There are also monadic and constrained variations of zipping available.)

Example: toList and zipWith

Suppose we want to write a function that translates records to JSON values, but allow the user per-field overrides which can change how the value of that field gets output. That is, we want to enable the user to provide a function of type

newtype FieldToJSON x = FieldToJSON (x -> Value)

for every field of type x. We will do this by providing a record of such functions to our JSON generation function, in addition to the actual record we want to translate:

recordToJSON :: KnownFields r => A.Record FieldToJSON r -> Record r -> Value
recordToJSON fs xs = Aeson.object . map (first fromString) $
    A.toList $ A.zipWith aux fs (S.toAdvanced xs)
  where
    aux :: FieldToJSON x -> I x -> K Value x
    aux (FieldToJSON f) (I x) = K (f x)

Function aux is returning K Value x, emphasizing that the result of aux is a Value, no matter what the type of the field was; this is what enables the call to toList.

It is worth noting quite how short and simple this function is; try doing this with regular records!

Applicative

Recall the types of pure and (<*>) from the prelude:

pure  :: Applicative f => a -> f a
(<*>) :: Applicative f => f (a -> b) -> f a -> f b

Records are “Applicative-like”, but don’t quite match this interface because, again, every field of the record has a different type. The corresponding functions in the advanced record API are:

pure  :: KnownFields r => (forall x. f x) -> Record f r
cpure :: AllFields r c => Proxy c -> (forall x. c x => f x) -> Record f r
ap    :: Record (f -.-> g) r -> Record f r -> Record g r

A function of type (f -.-> g) x is really a function from f x -> g x; thus, the type of ap says: “provided you have a record containing functions from f x -> g x for every field of type x in the record, and a corresponding record of arguments of type f x, then I can construct a record of results of type g x”.

Similarly, to construct a record in the first place, we can use pure or cpure. The type of pure is simpler, but it is less often useful: it requires the caller to construct a value of type f x for any x at all. Often that is not possible, and we need to know that some constraint c x holds; cpure can be used in this case.

If you have used large-generics or (more likely) sop-core before, you will find this style familiar. If not, this may look a little intimidating, but hopefully the examples in this blog post will help. You might also like to read the paper True Sums of Products where this style of programming was introduced.

Example: cpure

Our example JSON construction function took as argument a record of FieldToJSON values. In most cases, we just want to use toJSON for every field. We can write a function that constructs such a record for any row using cpure:

defaultFieldToJSON :: AllFields r ToJSON => A.Record FieldToJSON r
defaultFieldToJSON = A.cpure (Proxy @ToJSON) (FieldToJSON toJSON)

Suppose for the sake of an example that we want to generate JSON for our Config example, but that we want to output null for the header if it’s empty:

headerToJSON :: String -> Value
headerToJSON "" = Aeson.Null
headerToJSON xs = toJSON xs

Then

recordToJSON
  defaultFieldToJSON{header = FieldToJSON headerToJSON}
  defaultConfig

will result in something like

{
    "margin": 1,
    "fontSize": 18,
    "header": null
}

Example: ap

Suppose that we want the function that creates the value to also be passed the field name:

newtype NamedFieldToJSON a = NamedFieldToJSON (String -> a -> Value)

Our generation function must now zip three things: the record of functions, a record of names, and the actual record of values. We can get a record of names using

reifyKnownFields :: KnownFields r => proxy r -> Record (K String) r

(We will see reification and reflection of constraints in more detail when we discuss how to manually prove constraints.) However, large-anon does not offer a zipWith3. Not to worry; just like for ordinary Applicative structures we can write

pure f <*> xs <*> ys <*> zs

to combine three structures, we can do the same for records:

recordToJSON' :: forall r.
     KnownFields r
  => A.Record NamedFieldToJSON r -> Record r -> Value
recordToJSON' fs xs = Aeson.object . map (first fromString) $
    A.toList $
             A.pure (fn_3 aux)
      `A.ap` fs
      `A.ap` A.reifyKnownFields (Proxy @r)
      `A.ap` S.toAdvanced xs
  where
    aux :: NamedFieldToJSON x -> K String x -> I x -> K Value x
    aux (NamedFieldToJSON f) (K name) (I x) = K (f name x)

Traversable

The essence of Traversable is that we sequence effects: given some traversable structure of actions, create an action returning the structure:

sequenceA :: (Traversable t, Applicative f) => t (f a) -> f (t a)

We can do the same for records; the advanced API offers

sequenceA' :: Applicative m => Record m r -> m (Record I r)
sequenceA  :: Applicative m => Record (m :.: f) r -> m (Record f r)

and the simplified API offers

sequenceA :: Applicative m => A.Record m r -> m (Record r)

When we are sequencing actions, order matters, and large-anon guarantees that actions are executed in row-order (another reason not to consider rows “up to reordering”).

Example: sequenceA

Let’s go back to our Config running example, and let’s assume we want to write a parser for it. Let’s say that the serialised form of the Config is just a list of values, something like

2.1 14 Example

Then we could write our parser as follows (ANON_F is the equivalent of ANON for the advanced interface):

parseConfig :: Parser (Record Config)
parseConfig = S.sequenceA $ ANON_F {
      margin   = parseDouble
    , fontSize = parseInt
    , header   = parseString
    }

We are using sequenceA to turn a record of parsers into a parser of a record. However, what if the order of the serialised form does not match the order in the record? No problem, we can parse in the right order and then use project to reorder the fields:

parseConfig' :: Parser (Record Config)
parseConfig' = fmap S.project . S.sequenceA $ ANON_F {
      header   = parseString
    , margin   = parseDouble
    , fontSize = parseInt
    }

Of course, first ordering and then sequencing would not work!

Incidentally, anonymous records have an advance over regular records here; with normal records we could write something like

parseConfig :: Parser Config
parseConfig =
        MkConfig
    <$> parseDouble
    <*> parseInt
    <*> parseString

but there is no way to use the record field names with Applicative (unless we explicitly give the record a type constructor argument and then write infrastructure for dealing with it), nor is there an easy way to change the order.

Manually proving constraints

This section is aimed at advanced usage of the library; in most cases, use of the API we describe here is not necessary.

The large-anon type checker plugin proves KnownFields, AllFields and SubRow constraints, but only for concrete rows. When this is insufficient, the advanced interface provides three pairs of functions for proving each of these.

Inductive reasoning over these constraints is not possible. Induction over type-level structures leads to large ghc core size and bad compilation time, and is avoided entirely in large-anon.

Example: reflectAllFields

For reflectAllFields the pair of functions looks like this:

reifyAllFields   :: AllFields r c => proxy c -> Record (Dict c) r
reflectAllFields :: Record (Dict c) r -> Reflected (AllFields r c)

The former turns a constraint AllFields over a record into a record of dictionaries; the latter goes in the opposite direction. The only difference between Dict (defined in sop-core) and Reflected (defined in large-anon) is that the former takes a type constructor argument:

data Dict c a where
  Dict :: c a => Dict c a

data Reflected c where
  Reflected :: c => Reflected c

We’ll consider two examples. First, if a constraint c holds for every field in some larger record, then it should also hold for every field in a record with a subset of the larger record’s fields:

smallerSatisfies :: forall r r' c.
     (SubRow r r', AllFields r c)
  => Proxy c -> Proxy r -> Reflected (AllFields r' c)
smallerSatisfies pc _ =
    A.reflectAllFields $ A.project (A.reifyAllFields pc :: A.Record (Dict c) r)

Second, if a constraint c implies c', then if every field of a record satisfies c, every field should also satisfy c'. For example, Ord implies Eq, and hence:

ordImpliesEq :: AllFields r Ord => Reflected (AllFields r Eq)
ordImpliesEq =
    A.reflectAllFields $ A.map aux (A.reifyAllFields (Proxy @Ord))
  where
    aux :: forall x. Dict Ord x -> Dict Eq x
    aux Dict = Dict

Example: reflectSubRow

For the SubRow constraint, the pair of functions is

data InRow r a where
  InRow :: (KnownSymbol n, RowHasField n r a) => Proxy n -> InRow r a

reifySubRow   :: (KnownFields r', SubRow r r') => Record (A.InRow r) r'
reflectSubRow :: Record (A.InRow r) r' -> Reflected (SubRow r r')

For our final and most sophisticated example of the use of the advanced API, we will show how we can do a runtime check to see if one row can be projected to another. Such a check is useful when dealing with records with over existential rows, for example when constructing records from JSON values (see someRecord in the advanced API). The large-anon test suite contains contains an example of this in Test.Infra.DynRecord.Simple, as well as a slightly better version of checkIsSubRow in Test.Infra.Discovery.

Starting point

We want to write a function of type

checkIsSubRow ::
     (..)
  => proxy r1 -> proxy' r2 -> Maybe (Reflected (SubRow r1 r2))

We need to use reflectSubRow to do this, so we need to construct a record over r', where every field contains evidence that that field is a member of r.

Let’s consider how to do this one bit at a time, starting with perhaps a non-obvious first step: we will use reifySubRow to construct a record for r with evidence that every field of r is (obviously!) a member of r, and similarly for r':

checkIsSubRow _ _ =
    A.reflectSubRow <$> go A.reifySubRow A.reifySubRow
  where
    go :: A.Record (InRow r ) r
       -> A.Record (InRow r') r'
       -> Maybe (A.Record (InRow r) r')
    go r r' = ...

The strategy is now going to be as follows: we are going to try and translate the evidence of InRow r' to evidence of InRow r, by matching every field of r' with the corresponding field in r (if it exists).

Matching fields

In order to check if we have a match, we need to check two things: the field names need to match, and the field types need to match. For the former we can use

sameSymbol ::
     (KnownSymbol n, KnownSymbol n')
  => Proxy n -> Proxy n' -> Maybe (n :~: n')

from GHC.TypeLits, but to be able to do a runtime type check we need some kind of runtime type information. An obvious choice would be to use Typeable, but here we will stick with something simpler. Let’s suppose the only types we are interested in are Int and Bool; we can implement a runtime type check as follows:

data SupportedType a where
  SupportedInt  :: SupportedType Int
  SupportedBool :: SupportedType Bool

class IsSupportedType a where
  supportedType :: Proxy a -> SupportedType a

instance IsSupportedType Int  where supportedType _ = SupportedInt
instance IsSupportedType Bool where supportedType _ = SupportedBool

sameType :: SupportedType a -> SupportedType b -> Maybe (a :~: b)
sameType SupportedInt  SupportedInt  = Just Refl
sameType SupportedBool SupportedBool = Just Refl
sameType _             _             = Nothing

With this in hand, let’s now go back to our matching function. We have evidence that some field x' is a member of r', and we want evidence that x' is a member of r. We do this by trying to match it against evidence that another field x is a member of r, checking both the field name and the field type:

checkIsMatch :: forall x x'.
     (IsSupportedType x, IsSupportedType x')
  => InRow r' x' -> InRow r x -> K (Maybe (InRow r x')) x
checkIsMatch (InRow x') (InRow x) = K $ do
    Refl <- sameSymbol x x'
    Refl <- sameType (supportedType (Proxy @x)) (supportedType (Proxy @x'))
    return $ InRow x

Now for a given field x' of r', we need to look through all the fields in r, looking for a match:

findField :: forall x'.
      IsSupportedType x'
   => A.Record (InRow r) r -> InRow r' x' -> Maybe (InRow r x')
findField r x' =
    listToMaybe . catMaybes . A.collapse $
      A.cmap (Proxy @IsSupportedType) (checkIsMatch x') r

Finally, we just need to repeat this for all fields of r'; the full implementation of checkIsSubRow is

checkIsSubRow :: forall (r :: Row Type) (r' :: Row Type) proxy proxy'.
     ( KnownFields r
     , KnownFields r'
     , SubRow r  r
     , SubRow r' r'
     , AllFields r  IsSupportedType
     , AllFields r' IsSupportedType
     )
  => proxy r -> proxy' r' -> Maybe (Reflected (SubRow r r'))
checkIsSubRow _ _ =
    A.reflectSubRow <$> go A.reifySubRow A.reifySubRow
  where
    go :: A.Record (InRow r ) r
       -> A.Record (InRow r') r'
       -> Maybe (A.Record (InRow r) r')
    go r r' = A.cmapM (Proxy @IsSupportedType) (findField r) r'

Discussion: choice of InRow

Recall the type of reflectSubRow:

data InRow r a where
  InRow :: (KnownSymbol n, RowHasField n r a) => Proxy n -> InRow r a

reflectSubRow :: Record (A.InRow r) r' -> Reflected (SubRow r r')

This may look obvious in hindsight, but during development of the library it was far from clear what the right representation was for the argument to reflectSubRow; after all, we are dealing with two rows r and r', and it was not evident how to represent this as a single record.

When we finally settled on the above representation it intuitively “felt right”, and this intuition was confirmed in two ways. First, checkIsSubRow previously could only be defined internally in the library by making use of unsafe features; the library is now expressive enough that it can be defined entirely user-side. Indeed, Test.Infra.Discovery in the large-anon test suite also provides an example of the runtime computation of the intersection between two rows, again using safe features of the library only (turns out that this is a minor generalization of checkIsSubRow).

Secondly, if we look at the generated core for reflectSubRow (and clean it up a bit), we find

reflectSubRow d = unsafeCoerce $ fmap aux (toCanonical d)
  where
    aux (InRow _name index _proxy) = index

so we see that it literally just projects out the indices of each field, which is quite satisfying. In fact, if we didn’t include evidence of KnownSymbol in InRow then reflectSubRow would just be the identity function!

Indeed, the choice to include KnownSymbol evidence in InRow is somewhat unfortunate, as it feels like an orthogonal concern. Ultimately the reason we need it is that the kind of the type constructor argument to Record is k -> Type, rather than Symbol -> k -> Type: it is not passed the field names, and hence the field name must be an existential in InRow.

Internal representation

In this section we will give a short overview of the internal representation of a Record. The goal here is not to provide a detailed overview of the internals of the library, but rather to provide users with a better understanding of its runtime characteristics.

A Record is represented as follows:

data Record (f :: k -> Type) (r :: Row k) =
    NoPending  {-# UNPACK #-} !(Canonical f)
  | HasPending {-# UNPACK #-} !(Canonical f) !(Diff f)

We’ll consider the two cases separately.

No pending changes

When there are no pending changes (that is, updated or added fields), Record just wraps Canonical:

newtype Canonical (f :: k -> Type) = Canonical (StrictArray (f Any))
newtype StrictArray a = WrapLazy { unwrapLazy :: SmallArray a }

In addition, the evidence for RowHasField is just an Int:

class RowHasField (n :: Symbol) (r :: Row k) (a :: k) | n r -> a where
  rowHasField :: Tagged '(n, r, a) Int

This means that reading from a record in canonical form is just an array access, and should be very fast.

Pending changes

Updating is however an expensive operation, because the entire array needs to be copied. This is fine for small arrays, but this is not an approach that scales well. Record therefore represents a record with pending changes—added or updated fields—as a combination of the original array along with a Diff:

data Diff (f :: k -> Type) = Diff {
      diffUpd :: !(IntMap (f Any))
    , diffIns :: [FieldName]
    , diffNew :: !(SmallHashMap FieldName (NonEmpty (f Any)))
    }

The details don’t matter too much, but diffUpd contains the new values of updated fields, and diffIns records which new fields have been inserted; diffNew is necessary to deal with shadowing, which is beyond the scope of this blog post.

FieldName is a combination of a precomputed hash and the name of the field:

data FieldName = FieldName {
      fieldNameHash  :: Int
    , fieldNameLabel :: String
    }

instance Hashable FieldName where
  hash = fieldNameHash

These hashes are computed at compile time (through the KnownHash class, defined in large-anon).

The take-away here is that the performance of a Record will degrade to the performance of a hashmap (with precomputed hashes) when there are many pending updates. This makes updating the record faster, but accessing the record slower.

Applying pending changes

The obvious question then is when we apply pending changes, so that we have a flat array again. First of all, the library provides a function to do this:

applyPending :: Record f r -> Record f r

(and similary in the simplified interface). It might be advisable to call this function after having done a lot of field updates, for example. Of course, we shouldn’t call it after every field update because that would result in a full array copy for every update again.

The library also calls applyPending internally in two places:

• The ANON and ANON_F syntactic sugar call applyPending after the record has been constructed.
• All of the combinators on records (map, pure, zipWith, etc.) all call applyPending on any input records, and only construct records in canonical form. Since these operations are anyway O(n), the additional cost of calling applyPending is effectively hidden.

Benchmarks

So does all this work? Yes, yes it does, and in this section we will show a bunch of benchmarks to prove it. For a baseline, we will compare against superrecord; this is a library which has been optimized for runtime performance, but makes heavy use of type families and induction and consequently suffers from poor compilation times. It could certainly be argued that this is not the library’s fault, and that ghc should do better; for now, however, we must work with what we have. It should also be noted that unlike large-anon, superrecord does treat rows “up to reordering”.

Record construction

In superrecord there are two ways to construct records: a safe API (rnil and rcons), and an unsafe API (unsafeRNil and unsafeRCons). The latter is unsafe in two ways: unsafeRNil must be told how much space to allocate for the record, and unsafeRCons does in-place update of the record, potentially breaking referential transparency if used incorrectly.

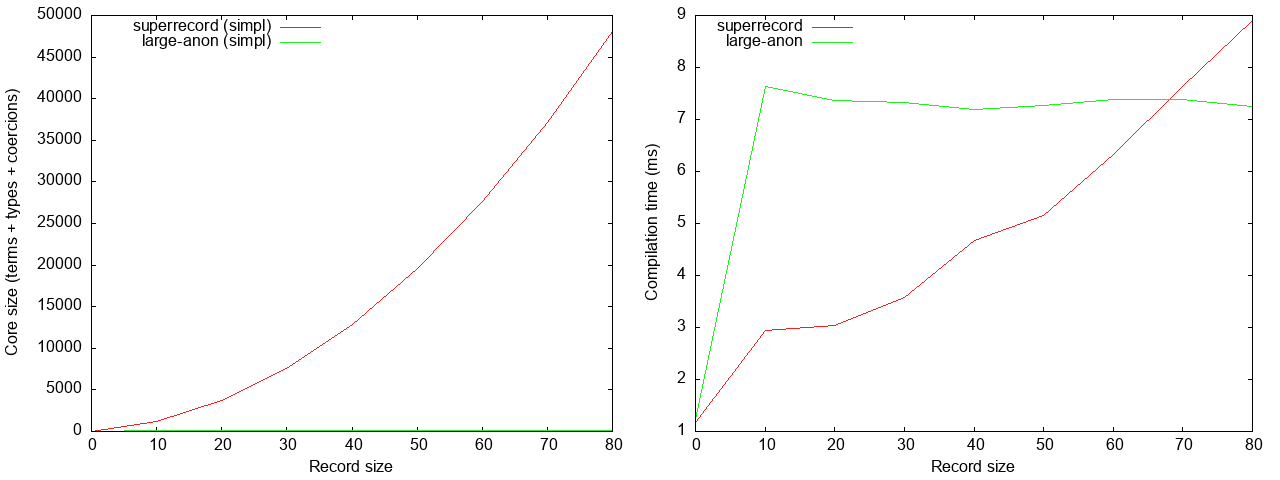
The safe API has such bad compilation time performance that we effectively cannot compare it to large-anon. By the time we get to records of 40 fields, we end up with a ghc core size of 25 million AST nodes (terms, types and coercions), and it takes 20 seconds to compile a single record; this time roughly doubles with every 10 more fields.

We will instead compare with the unsafe API:

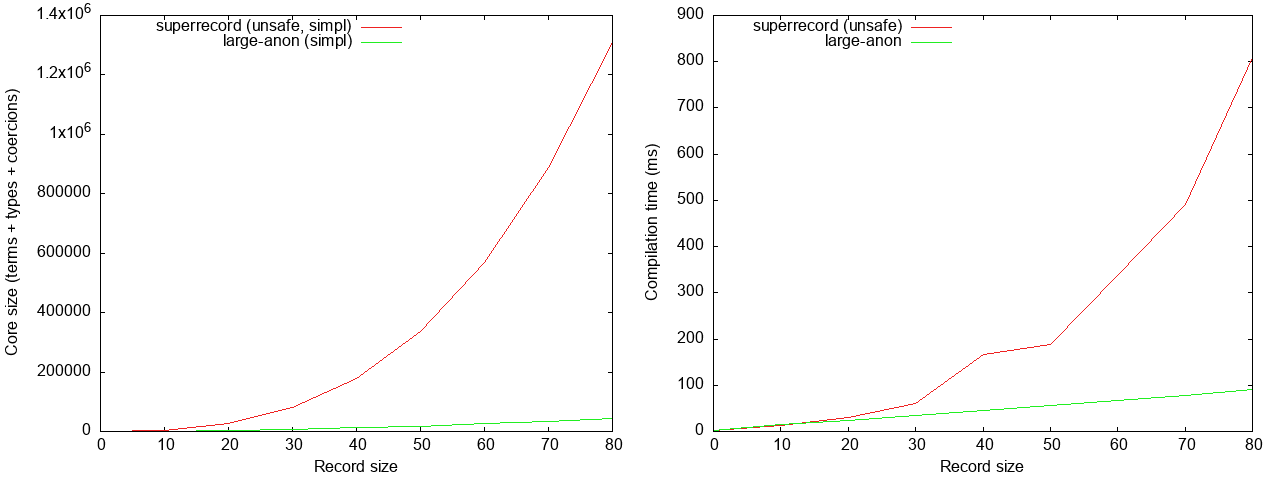
We see that for records with 80 fields, large-anon results in ghc core that is roughly an order of magnitude smaller, and compilation time that is about 5.5x faster. The left graph here might suggest that the ghc core size generated by large-anon is linear in the size of the record; this is not quite the case:

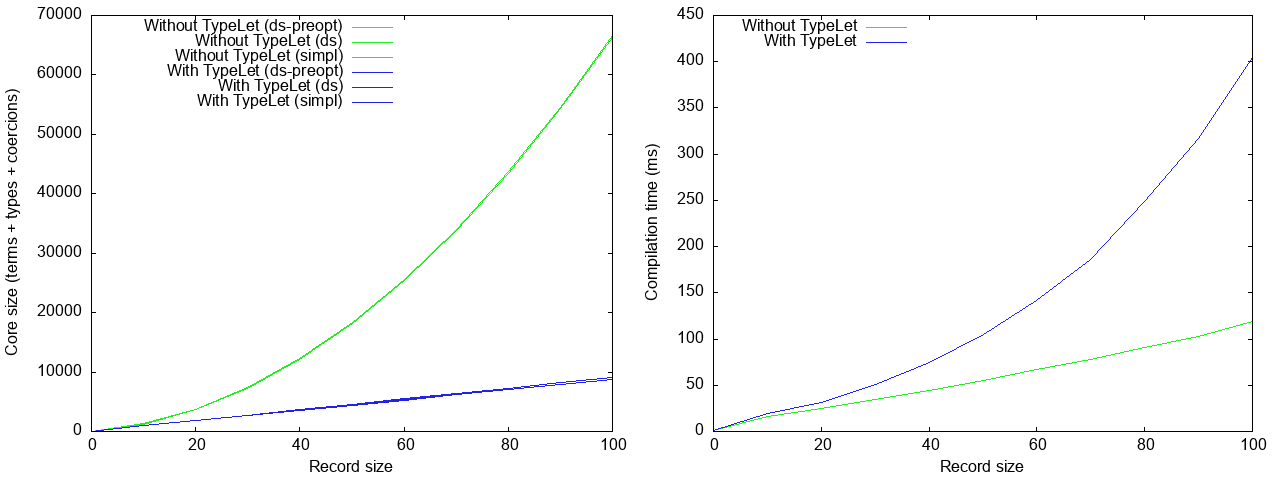
(We are showing the core size after desugaring, the very simple optimizer, and the simplifier, but in this case all three are basically of identical size.) The green line is what large-anon does out of the box, and we see that it is not linear. The reason is that repeated calls to insert result in O(n²) type arguments (see Avoiding quadratic core code size with large records for a detailed discussion of this problem). We do have experimental support for integration with typelet (see Type-level sharing in Haskell, now), and while does indeed result in ghc core that is linear in size (blue line), unfortunately it actually makes compilation time worse (although still very good) – at least for this benchmark. Fortunately, compilation time without typelet is linear (again, for this benchmark).

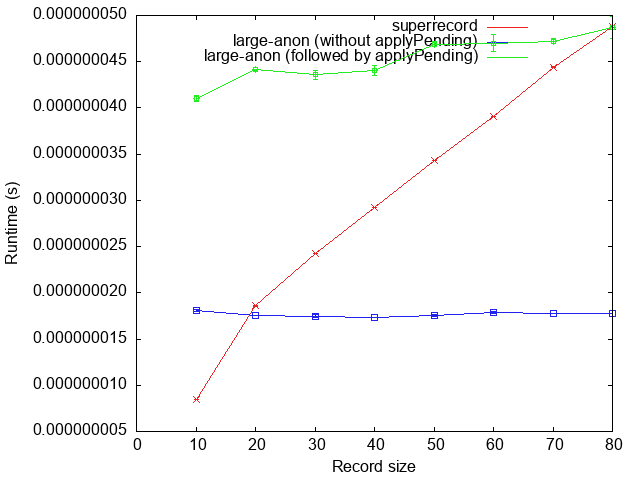
The runtime performance of superrecord is much better, of course:

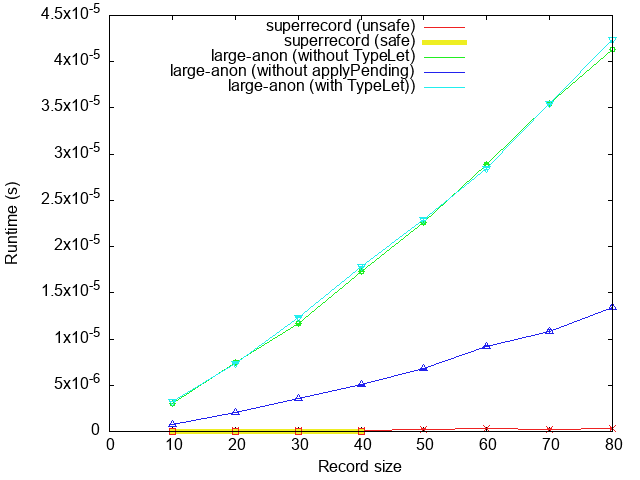
The most relevant lines here are the red line (unsafe superrecord API) and the green line (default large-anon: no typelet integration, and with a call to applyPending after the record is constructed). We see that superrecord is significantly faster here, by roughly two orders of magnitude. This is not surprising: large-anon first builds up a Map, and then flattens it, whereas superrecord just constructs a single array and then updates it in place (albeit in an unsafe manner).

Accessing record fields

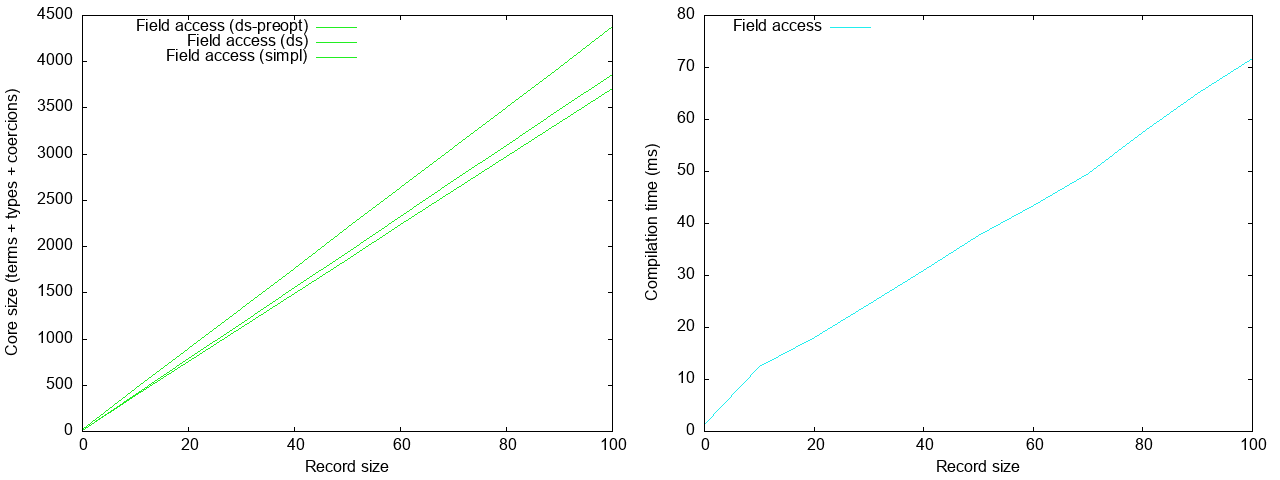
Let’s now consider the performance of reading a bunch of fields from a record. The benchmark here constructs a function that extracts half of the fields of a record (into a non-record datatype).

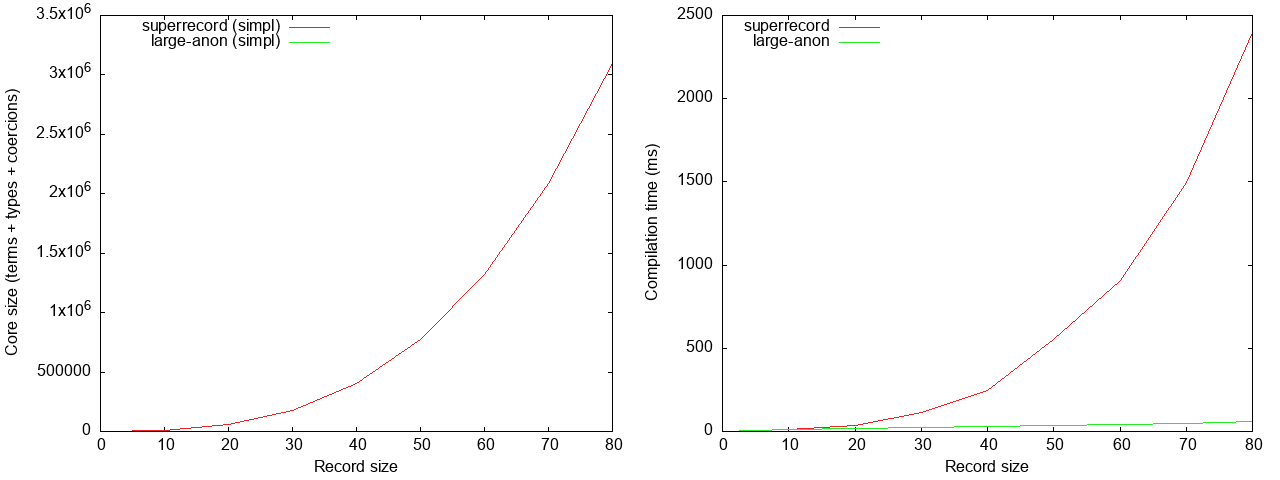
The ghc core size in large-anon is so small that is is entirely dwarfed by superrecord; it is in fact linear, going up to roughly 3,500 AST nodes for a record of 80 fields, about 3 orders of magnitude better than superrecord. Compilation time is similarly much better, by more than an order of magnitude (50 ms versus 2.5 seconds), and also linear. Showing just large-anon by itself:

Comparing runtime is a bit more difficult, because of the hybrid representation used by large-anon: it very much depends on whether the record has many pending changes or not. We will therefore measure the two extremes: when the record has no pending changes at all, and when the record consists entirely of pending changes, with an empty base array:

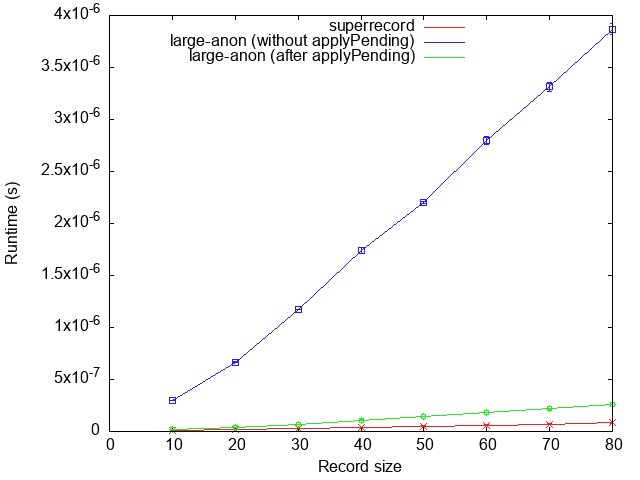
Note that when the record is in canonical form (green line), large-anon and superrecord have very similar performance; large-anon is slower by roughly a factor 2x, which can be explained by having to check whether the record is in canonical form on every field access. At the other extreme (blue line), large-anon again degrades to the performance of a Map and is therefore about an order of magnitude slower. Actual performance in any application will fall somewhere between these two extremes.

Updating record fields

The hybrid nature of large-anon here too makes a direct comparison with superrecord a bit difficult. The performance of updating a single field will be different to updating many, and will depend on whether or not we call applyPending. We will therefore show a few different measurements.

Let’s first consider updating a single field. Both superrecord and large-anon have good compilation time performance here; superrecord is non-linear, but in this benchmark we don’t really notice this because compilation is essentially neglible:

In terms of runtime, however, since superrecord needs to copy the entire array, we expect large-anon to do better here:

Indeed, updating a single field has a constant cost in large-anon, since it just adds a single entry to the map.

Of course, in practice we will eventually want to update a bunch of fields, and then call applyPending, so let’s measure that too. First, compilation time:

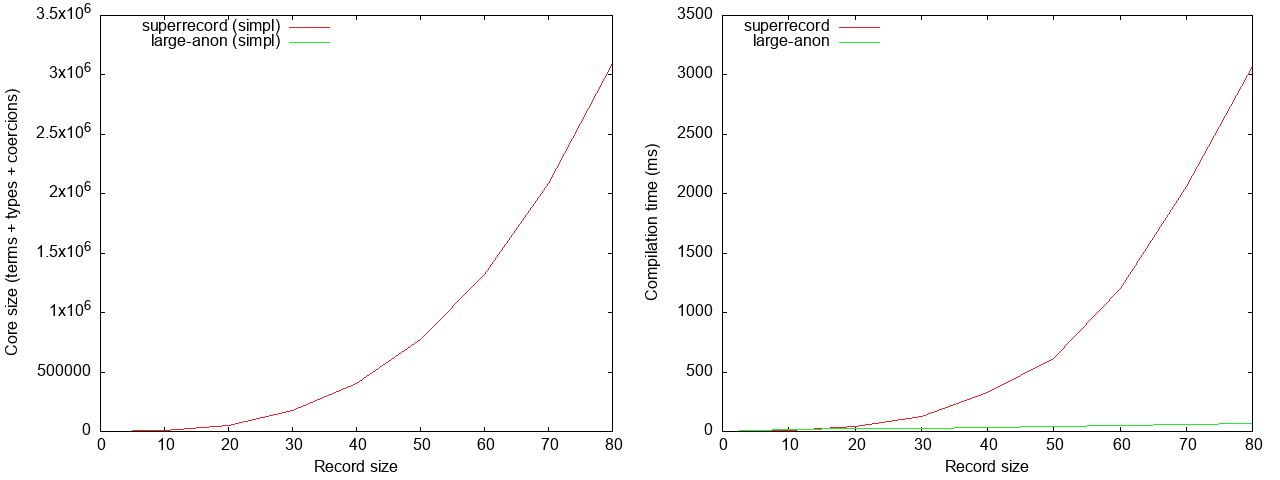
Here the non-linear compilation time of superrecord really becomes noticable; for a record of 80 fields, it is again more than an order of magnitude slower (50 ms versus 2.5 seconds).

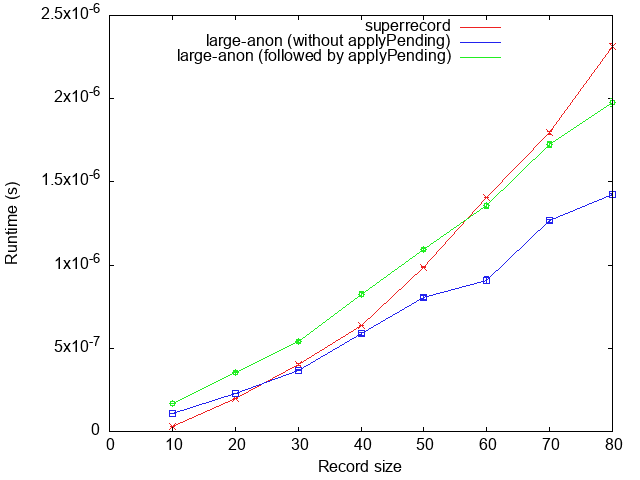
At runtime, field update in large-anon is slightly slower than superrecord for small arrays, but does better than superrecord for larger records. After all, every single field update results in an full array copy in superrecord, which is inherently O(n²). By contrast, large-anon merely updates the map, and then flattens it out at the end, constructing a single array. This is more expensive for smaller arrays, but is O(n log n) instead and therefore scales and becomes faster for larger arrays. Of course, it does mean that applyPending must be called at an appropriate moment (see Applying pending changes).

We should emphasize again that the goal of large-anon was not to create a library that would be better than superrecord at runtime, but rather to create a library with good enough runtime performance but excellent compile time performance. Nonetheless, the O(n²) vs O(n log n) cost of updating records may be important for some applications. Moreover, all functions in large-anon that work with entire records (functions such a (c)map and co) are all O(n).

Generics

There is no explicit support for generics in superrecord, but it does support conversions between records and JSON values. We will compare this to the JSON conversion functions in large-anon, which are defined in terms of generics (indeed, they are just the functions defined in large-generics). Thus, toJSON will serve as an example of a generic consumer, and parseJSON as an example of a generic producer. If anything this benchmark is skewed in favour of superrecord, because what we are measuring there is the performance of more specialized functions.

Let’s first consider the generic consumer, i.e., toJSON:

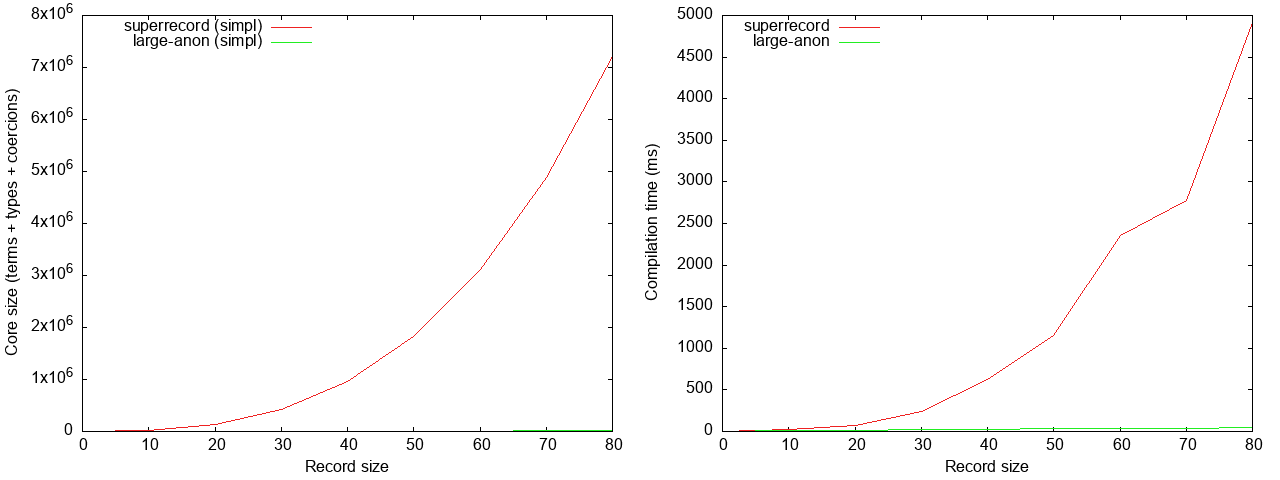
The ghc core size and compilation time of large-anon get dwarfed here by those of superrecord, so let’s consider them by themselves:

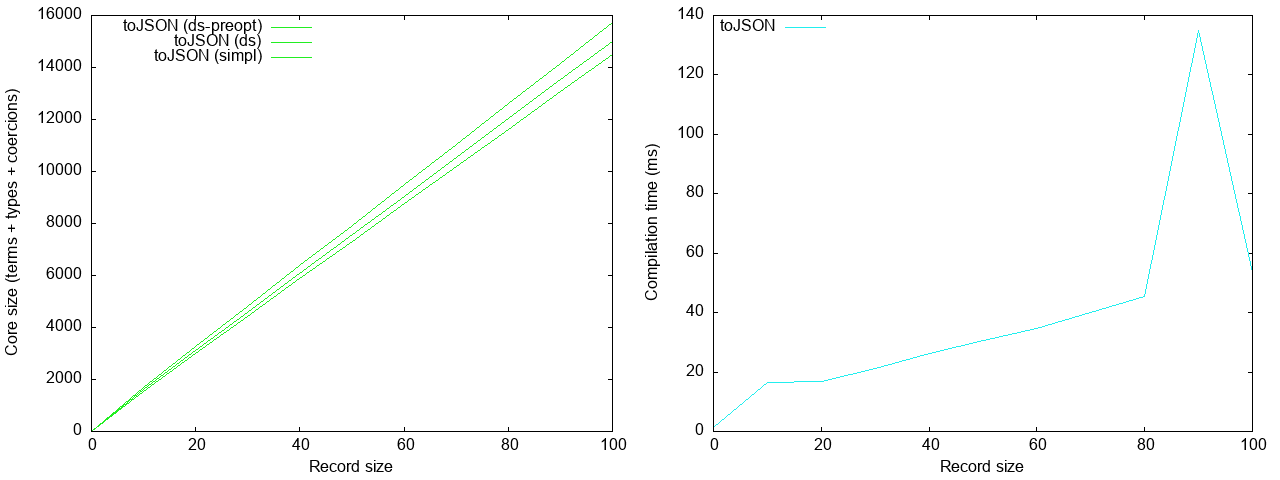
We see that the ghc core size in large-anon is beautifully linear, and so is compilation time.⁴ Moreover, compilation time is roughly two order of magnitude faster than superrecord (60 ms versus 6 seconds).

Runtime performance:

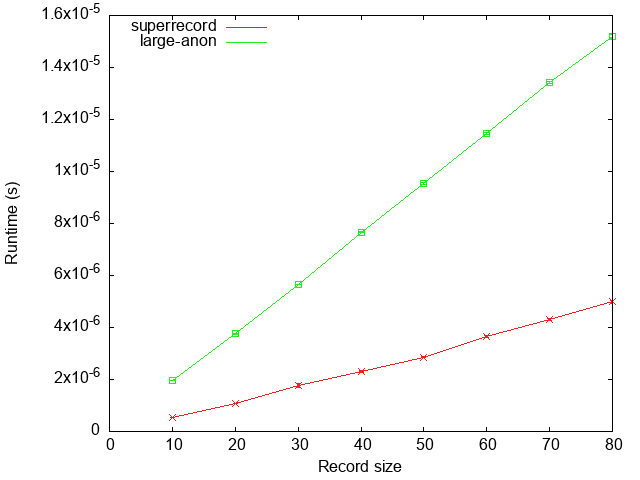
We see that large-anon is a little more than 2x slower than superrecord, quite an acceptable performance for a generic function.

Finally, the generic producer, i.e., parseJSON:

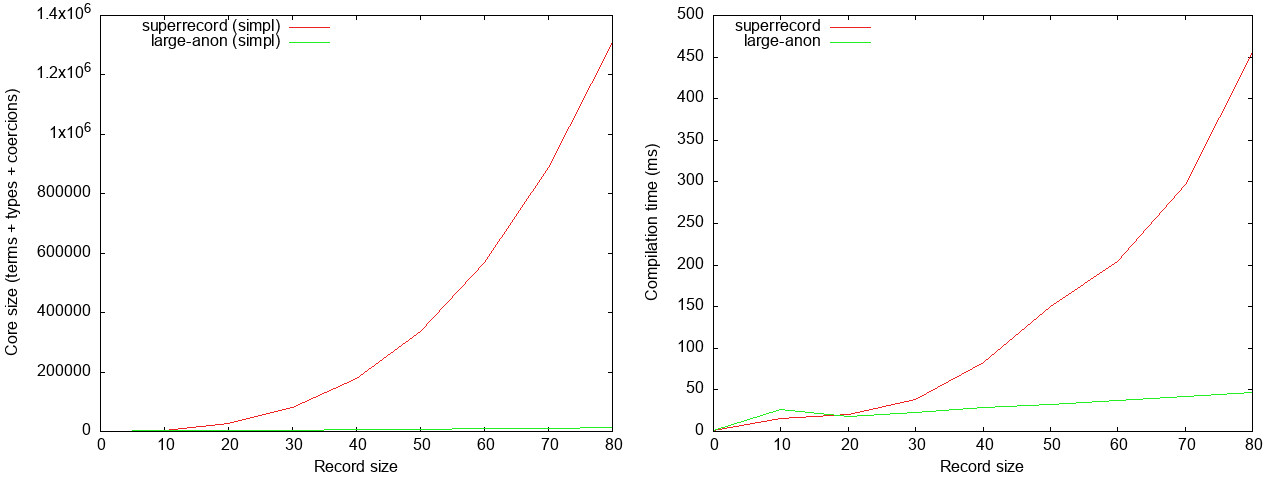
Here the different in compile time is less extreme, but large-anon is still roughly an order of magnitude faster (with much, much smaller ghc core). Runtime:

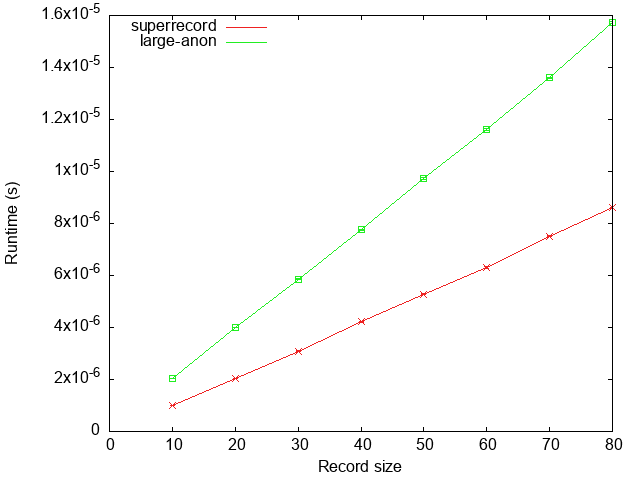
We see that superrecord is again roughly 2x faster (slightly less).

Conclusions

The large-anon library provides anonymous records for Haskell, which are

• practical: the library comes with good syntactic sugar and a very expressive API.
• scalable: compilation time is linear in the size of records.

For records with 80 fields, compilation time is somewhere between one and two orders of magnitude faster than superrecord. For runtime performance of reading record fields, large-anon lies somewhere between superrecord and Data.Map; for writing record fields and generic operations, large-anon is up to roughly 2x slower than superrecord, but sometimes much faster. The runtime performance of the library can almost certainly be improved; the focus has been on excellent compilation time performance, not excellent runtime performance. That said, I would be pretty certain that for nearly all applications the runtime performance of large-anon is just fine.

The development of large-anon is the latest, and for now probably final, installment in our research on improving compilation time on behalf of Juspay; see the blog posts tagged with compile-time-performance for everything we have written on this topic. In addition, the large-records repo contains a detailed benchmarks report, covering large-records, large-anon, and typelet, as well as the various individual experiments we have done. In addition to documenting the research, perhaps this can also help research into compilation time by other people. We are thankful to Juspay for sponsoring this research and improving the Haskell ecosystem.

Other features

We have covered most of the library’s features in this blog post, but not quite all:

• All examples of the advanced API in this blog post have been over rows of kind Type (*). The actual API is kind polymorphic; Test.Sanity.PolyKinds in the large-anon test suite contains an example of records with types like this:

  Record Boxed ["a" := Lazy Bool, "b" := Strict Int]

  This is taking advantage of kind polymorphism to differentiate between strict and lazy fields. (In practice this is probably overkill; large-anon is strict by default; to get lazy fields, just use a box data Box a = Box a.)

  Indeed, the runtime functions on rows such as checkIsSubRow (see section Example: reflectSubRow above) are also entirely kind polymorphic, and as demonstrated in Test.Infra.DynRecord.Advanced, row discovery for existential records also works for kinds other than Type.

• Records can also be merged (concatenated):

  merge :: Record f r -> Record f r' -> Record f (Merge r r')

  The Merge type family does not reduce:

  example :: Record Maybe (Merge '[ "a" :=  Bool ] '[])
  example = merge (insert #a (Just True) empty) empty

  HasField constraint can be solved for rows containing applications of Merge, and project can be used to flatten merged records:

  example :: Record Maybe '[ "a" :=  Bool ]
  example = project $ merge (insert #a (Just True) empty) empty

• We have not covered the full set of combinators, but hopefully the Haddock documentation is helpful here. Moreover, the set of combinators should be entirely familiar to people who have worked with large-generics or sop-core.

• In principle the library supports scoped labels. After all, insert has no constraints:

  insert :: Field n -> f a -> Record f r -> Record f (n := a : r)

  The absence of any constraints on insert means that a sequence of many calls to insert to construct a large record is perfectly fine in terms of compilation time, but it also means that fields inserted later can shadow fields inserted earlier. Indeed, those newer fields might have different types than their older namesakes. Everything in the library is designed to take this into account, and I believe it makes for a simpler and more uniform design.

  However, the library currently offers no API for making shadowed fields visible again by removing the field that is shadowing them. There is no fundamental reason why this isn’t supported, merely a lack of time. The work by Daan Leijen in scoped labels (for example, Extensible records with scoped labels) may provide some inspiration here.

Alternative approaches

In a previous blog post Induction without core-size blow-up: a.k.a. Large records: anonymous edition we discussed some techniques that can be used to do type-level induction in Haskell without resulting in huge ghc core and bad compilation time. The reason we ended up not going down this path in the end for large-anon was primarily one of usability.

Consider checking whether a field is a member of a (type-level) row. If the row is a list, then the search is necessarily O(n). If we want to reduce this to O(log n), we could index records by type-level balanced trees. We explored this to some degree; in fact, we’ve gone as far as implementing guaranteed-to-be-balanced type-level red-black trees. In the end though this results in a poorer user experience, since these type-level trees then appear in user visible types, error messages, and so on.

Using a plugin resulted in a more practical library. Note, though, that we are using a plugin only for better compile time performance. In principle everything that large-anon does could be done with type families within Haskell itself; this is different to plugins such as Coxswain which really try to implement a theory of rows. The large-anon library does not attempt this; this keeps the library more simple, but also more predictable. For example, we have seen various examples above that having rows be ordered is useful.