This post originally appeared on Edsko’s personal blog.
There are many blog posts and descriptions of blockchain technology on the web, but I feel that very few of them get to the heart of the matter: what is the fundamental problem that blockchains solve? In this blog post I want to take a look at this question; this blog post is intended for a general audience and I will assume no technical knowledge. That does not mean however that we will need to dumb things down; we will see what the fundamental problem solved by blockchain is, and we will even see two alternative ways in which this problem is solved, known as proof-of-work (used by for example Bitcoin) and proof-of-stake (used by for example the Cardano blockchain).
Full disclosure: I was one of the lead engineers on the Cardano blockchain, where I worked on the wallet specification, researched coin selection, designed the architecture of the consensus layer and wrote the hard fork combinator. This blog post is however just my personal perspective.
Motivation
Suppose a group of people want to share information with each other. The nature of that information does not really matter; for the sake of having an example, let’s say it’s a group of companies who want to share supply availability, purchase orders, etc. How might we go about setting up a system to make this possible?
Bulletin board
As a starting point, perhaps we could just set up a server where everybody
can post messages and everybody can see everybody else’s messages.
For reasons that will become clear later, we will refer to the messages that
users post as blocks: users can post arbitrary blocks of data.1
Suppose we have some suppliers A, B, C, ..; they might be posting blocks
(messages) such as this:
| Number | Block contents |
|---|---|
| 0 |
A has 1000 sprockets available
|
| 1 |
B has 500 springs available
|
| 2 |
A looking for a supplier of 300 springs
|
| 3 |
C agrees to buy 100 sprockets from A at €2/sprocket
|
(Block numbers added just for clarity, they are not part of the block itself.)
Systems like this are basically just some kind of bulletin board and have been around in digital form since before Internet times, and obviously in non-digital form basically forever.
Signatures
Naturally, the problem with this system is that nothing is preventing people from posting messages that aren’t true. For the system to be useful as a supply chain system, suppliers must be able to depend on the messages that get posted. An important and obvious first step towards addressing this problem is to require messages to be signed. Digital signatures are a well-understood problem; the exact details of how it’s done don’t really matter.
With the addition of signatures, the server might now look something like this:
| Block contents | Signed by |
|---|---|
A has 1000 sprockets available
|
A
|
B has 500 springs available
|
B
|
A looking for a supplier of 300 springs
|
A
|
C agrees to buy 100 sprockets from A at €2/sprocket
|
A, C
|
Replay attacks
The addition of signatures is a big improvement, but it’s not yet sufficient.
For example, perhaps A agreed to sell 100 sprockets to C at €2/sprocket
only as a once-off; maybe it was some kind of special introductory price. The
fact that A agreed to do this once does not necessarily mean that A will
agree to do it again, but in our system so far nothing is stopping C from
reposting the message again:
| Block contents | Signed by |
|---|---|
A has 1000 sprockets available
|
A
|
B has 500 springs available
|
B
|
A looking for a supplier of 300 springs
|
A
|
C agrees to buy 100 sprockets from A at €2/sprocket
|
A, C
|
| other messages | |
C agrees to buy 100 sprockets from A at €2/sprocket
|
A, C
|
After all, the message is signed by both A and C and so it looks legit.
This is known as a replay attack, and there are many ways to solve it. Here
we will consider just one way: we will introduce an explicit ordering; as will
see, this will be important later as well.
To introduce an ordering, each block will record the hash of its predecessor block. You can think of a hash of a block as a mathematical summary of the block: whenever the block changes, so does the summary.
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 5195 | none |
A has 1000 sprockets available
|
A
|
| 5843 | 5195 |
B has 500 springs available
|
B
|
| 2874 | 5843 |
A looking for a supplier of 300 springs
|
A
|
| 9325 | 2874 |
C agrees to buy 100 sprockets from A at €2/sprocket
|
A, C
|
Crucially, the signature also covers the block’s predecessor; this is what is
preventing the replay attack: C cannot post the same message again, because
if they did, that new block must have a new predecessor, and that would then
require a new signature:
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 5195 | none |
A has 1000 sprockets available
|
A
|
| 5843 | 5195 |
B has 500 springs available
|
B
|
| 2874 | 5843 |
A looking for a supplier of 300 springs
|
A
|
| 9325 | 2874 |
C agrees to buy 100 sprockets from A at €2/sprocket
|
A, C
|
| 9325 | other messages | ||
| … | |||
| 6839 | |||
| 7527 | 6839 |
C agrees to buy 100 sprockets from A at €2/sprocket
|
??? |
Notice how this is creating a chain of blocks: every block linked to its predecessor. In other words, a block chain; although what we have described so far isn’t really a blockchain in the normal sense of the word just yet.
Eliminating the central server
So far all messages have been stored on some kind of central server. One worry we might have here is what happens when that server goes down, suffers a hard disk failure, etc. However, server replication, data backup, etc. are again well-understood problems with known solutions; that won’t concern us here.
A more important question is: what happens if we cannot trust the central server? First, notice what the server can not do: since messages are signed by users, and the server cannot recreate those signatures, it is not possible for the server to forge new messages. The server can however delete messages, or simply not show all messages to all users.
Let’s first consider why the server might even want to try. Suppose the server currently has the following blocks:
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 2547 | none |
A has 1000 sprockets available
|
A, B, C
|
| 8861 | 2547 |
A agrees to sell 800 sprockets to B
|
A
|
In this example, A declares to have a sprocket supply, and both B and C
have ratified the message. Now when A agrees to sell sprockets to B, B
knows that A actually has these sprockets available, and so might transfer
the money for the sprockets to A. If A tries to sell the sprockets to
both B and C, C will know something is amiss:
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 2547 | none |
A has 1000 sprockets available
|
A, B, C
|
| 8861 | 2547 |
A agrees to sell 800 sprockets to B
|
A
|
| 1010 | 8861 |
A agrees to sell 800 sprockets to C
|
A
|
If A only has 1000 sprockets, they can’t be selling 800 sprockets to both
B and C. But suppose the server is in cahoots with A, and simply doesn’t
show the transaction with B to C; in other words, the chain that the server
might present to C could be
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 2547 | none |
A has 1000 sprockets available
|
A, B, C
|
| 6079 | 2547 |
A agrees to sell 800 sprockets to C
|
A
|
Now C doesn’t know that anything is wrong. This way A can basically sell
their stock to as many people as they want, collect the money, and disappear.
This is known as a double spending attack, and we cannot fix it if we stick
with a central server: after all, the chains that B and C see are both
perfectly reasonable and plausible; the attack consists of showing a different
chain to different users, even though the chain that each user sees is itself
valid. As we will see, this is the problem that the blockchain solves.
Revising history
Before we get to the real blockchain, however, we should discuss one more thing.
Consider again the example from the previous section, where the server is
untrustworthy, and is cooperating with A to dupe both B and C. Unlike in
the previous example, however, suppose that the transaction with A was not the
last transaction on the chain; perhaps the server looks like this instead:
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 2547 | none |
A has 1000 sprockets available
|
A, B, C
|
| 8861 | 2547 |
A agrees to sell 800 sprockets to B
|
A
|
| 3598 | 8861 | Some other message |
D
|
If the server now wants to present an alternative chain to C, in which A
is selling the sprockets to C instead of to B, it cannot include the
message signed by D. The message signed by D records the hash of its
predecessor; if the server changes that predecessor (A selling to C instead
of A selling to B), it would have a different hash, and would therefore
require a new signature:
| Hash | Pred | Block contents | Signed by |
|---|---|---|---|
| 2547 | none |
A has 1000 sprockets available
|
A, B, C
|
| 6079 | 2547 |
A agrees to sell 800 sprockets to C
|
A
|
| 4592 | 6079 | Some other message | ??? |
However, this unfortunately does not help us. First of all, notice that the
server could simply truncate the chain and not include the message signed by D
when presenting the chain to C. Moreover, even when the chain does include
additional messages, messages earlier on the chain are still not trustworthy.
The problem is that we don’t know who D is. Perhaps D is the server itself;
if so, then the existence of a message signed by D tells us nothing. Indeed,
in the final example above, the server could just construct a new signature in
the place of the “???”.
Proof of work: solving puzzles
If we cannot trust the central server, perhaps we can simply allow everyone to produce blocks. Everyone keeps a copy of the block chain, and when someone wants to add a message to the chain they just create it themselves and send it everybody else. If two people happen to create a block at the same time, no problem: we just pick one of the two blocks, and whoever “lost” will just create a new block on top of the block that got adopted, no big deal.
This by itself does not solve anything just yet. A could just take the block
that contains the transaction with B and send it to B but not to C, and
vice versa. Just like before, even if B and C would wait for additional
blocks to be added on top of the block they just received, they have no
guarantee that those blocks are not being produced by nodes that are cooperating
with A.
To even have a chance of having a way out of this impasse we will need to impose an assumption: although some participants may be untrustworthy, we will assume that the majority is honest. In the previous section we saw that once the chain includes an honest block, untrustworthy participants can no longer revise the blockchain’s history. Therefore, if the blockchain is operating normally, every new block that comes in increases the likelihood that the chain contains an honest block. After a while the probability that the most recent k blocks on the chain (for some number k) does not contain any honest block is so small that any information that is older than k can be considered trustworthy.2
Unfortunately, while the assumption that the majority of the participants is honest may seem reasonable, that does not mean that we can assume that the majority of the blocks we receive are produced by honest participants. After all, nothing is stopping untrustworthy participants from producing lots and lots of blocks. Unless… we introduce something that does stop that.
Puzzles
This was the genius insight behind Bitcoin: we can translate the assumption “the majority of participants is honest” to “the majority of blocks is honest” if blocks are costly to produce. In order to produce a block, the block must solve a particular mathematical puzzle. It does not really matter what the puzzle is exactly, except that (1) it takes a computer a long time to solve, and (2) we can verify that the solution is correct very quickly. The answer to this puzzle is called proof of work (proof that you did the work that makes a block computationally expensive to produce), and must be included in every block:
| Hash | Pred | Proof of work | Block contents | Signed by |
|---|---|---|---|---|
| 2547 | none |

|
A has 1000 sprockets available
|
A, B, C
|
| 8861 | 2547 |

|
A agrees to sell 800 sprockets to B
|
A
|
| 3598 | 8861 |

|
Some other message |
D
|
Notice how this prevents dishonest nodes from producing lots of different blocks: they would have to solve lots of different puzzles, which would simply be impossible in the time available. We do have to make our “honest majority” assumption a bit more precise for this to be viable: we must assume that the honest participants have more puzzle solving power than the dishonest participants; roughly speaking, the honest participants together must have more powerful computers than the dishonest participants.
This means that provided the honest participants are producing blocks, the blocks we receive over the network have at most a 50% probability of being produced by dishonest participants, and therefore the probability that no block is produced by an honest particant diminishes quickly; after 100 blocks that probability is roughly .000000000000000000000000000001.
Chain selection
We mentioned above that it’s possible that two participants produce a block at
the same time; when this happens, we just pick one arbitrarily, and continue;
the participant who “lost” just produces a new block on top of the block that
got picked, and we continue. It is possible that we discover this clash a bit
later. For example, suppose B and C produce a block at the same time, D
only sees the block produced by B and adds their block on top of Bs block:
| 5285 | none |

|
.. |
A
|
||||||||||
| 7115 | 5285 |

|
.. |
A
|
||||||||||
| 1413 | 7115 |

|
.. |
B
|
5980 | 7115 |

|
.. |
C
|
|||||
| 6679 | 1413 |
|
.. |
D
|
||||||||||
This is known as a fork in the blockchain. If all nodes are honest, how we resolve the fork does not actually matter terribly: as long as everybody applies the same rule, we end up with the same chain, and the blocks that “lost” are just reconstructed on the new fork. However, we want to throw away as little work as possible, and so we will opt to select the longest chain. More importantly, if the fork was intentionally produced by a dishonest participant, then picking the longer fork also gives us a higher probability of picking the fork with more blocks produced by honest participants: after all, in order to produce the longer fork, more puzzles had to be solved. We say that the difficulty of producing a chain increases with its length.
Proof of stake
Although the introduction of the puzzles was a genius insight, it does have one very important drawback: it is extremely wasteful. A study in 2014 found that the global production of blocks on the Bitcoin block chain consumed as much energy as the entire country of Ireland.3 In a world where energy consumption is one of the greatest challenges to face mankind, this is obviously not a sustainable solution.
The key insight is that the important feature of proof-of-work is not necessarily that it is costly to produce blocks, but rather that we tie block production to some kind of resource of which participants have a limited amount. In proof of work that resource happens to puzzle solving (compute) power, but other choices are possible as well. In particular, most blockchains themselves are recording some kind of resource that is tied to a real-world resource: if the blockchain is supporting a cryptocurrency, then the amount of crypto someone owns can be considered their resource; for our running example, we could consider the amount of supplies that someone offers on the blockchain to be their resource.4
Let’s say someone owns 10% of all resources on the chain (i.e., they own 10% of the cryptocurrency, or in our example, 10% of the available supplies is theirs); we then say that they have a 10% stake. In a proof-of-stake blockchain, the probability that someone is allowed to produce a block is proportional to their stake: users with little stake can only produce a few blocks, users with a lot of stake can produce many. Our “honest majority” assumption now becomes: provided that the honest participants have more than 50% stake in the system, the probability that any block is produced by a dishonest participant will be less than 50%, just as for proof-of-work.
Leadership schedule
There are many ways to construct a proof-of-stake blockchain; what I will describe here is based on the Ouroboros consensus protocol5, the consensus protocol underlying the Cardano blockchain.
Here’s how a proof of stake blockchain works. Time is divided into slots; for simplicity, we can think of slots as just being equal to seconds (indeed, on the Cardano chain one slot takes one second), and slots are grouped into epochs; on the Cardano chain, one epoch contains a little under half a million slots, for a total of 5 days.6 At the start of each epoch, we run a lottery for each slot in the next epoch. Most of those slots will be empty7, but for some slots we will assign a slot leader: the participant that is allowed to produce a block for that slot. The details of how this lottery works are not very important for our current purposes, except to say that there are clear rules on how to run the lottery that every participant on the chain will follow and cannot really tamper with.
The only way for an dishonest participant to increase how many blocks they can produce is to increase their stake in the system. However, this has real life consequences: depending on how “stake” is defined exactly, it might mean they have to buy cryptocurrency, make more supply stock available, etc. Provided that the real world consequences of increasing stake are more than the potential benefit from attempting an attack on the system, the system is secure.
Put another way, participants with the most stake in the system are also most invested in the system: they need the system to succeed and continue to operate. Therefore, they are more trustworthy than nodes with less stake.
Chain selection
Since block production is no longer costly (the whole point was to avoid wasteful energy consumption after all), it is not difficult for dishonest participants to construct long chains. Therefore if we have to choose between two chains, choosing the longer chain may not necessarily be the right choice. Instead, we will look at chain density. Suppose we have to choose between two chains:
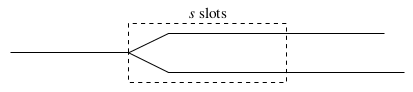
We will count the number of blocks on each chains in a window of s slots; the
exact value of s does not matter so much; let’s say s is 100,000 blocks.8
Recall the shape that the “honest majority” assumption takes in a proof-of-stake
blockchain: the honest majority has more than 50% stake in the system. That
means that within the window, the chain produced by the honest participants
in the system will contain more blocks than the chain produced by dishonest
participants. Therefore, whenever there is a fork in the chain, we must pick
the chain that is denser (contains more blocks) in a window of slots at
the intersection point. This is known as the Ouroboros Genesis rule.9
There is a useful special case for this rule. The mathematical analysis of
the Ouroboros protocol10 tells us that when all participants in the
network are following the protocol, their chains might be a little different
near the tip (because not all forks are resolved yet), but the intersection
point between all those chains will be no more than k blocks back. Moreover,
blocks for “future” slots (slots that we haven’t reached yet11) are
considered invalid. In other words, the situation looks a bit like this:
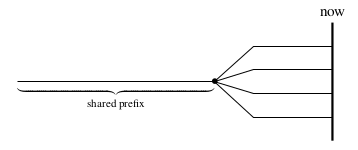
where none of the chains can exceed past “now”. In this case, the densest chain in the window will also be the longest; this means that for nodes that are up to date, the longest chain rule (just like in proof of work) can be used. Indeed, this is the rule in Ouroboros Praos, albeit with a side condition; for the details, please see my chapter “Genesis” in the Cardano Consensus Layer Report.
Conclusions
Allowing a group of people to share information is not a difficult problem to solve; techniques such as digital signatures as well as ways to address replay attacks are well understood problems. Things get a lot trickier however if we drop the assumption that we can trust the server on which the data is stored. Although the server cannot manufacture data, it can selectively omit data. Detecting and guarding against this is very difficult: after all, when the server omits data, it is simply going back to an earlier state of the chain, in which that data was not yet present. Therefore almost by definition the version of the chain with some parts omitted must also be valid.
The solution to this is to allow all participants in the network to produce blocks. When we do that, we must have a way to resolving conflicts: when two or more nodes produce a block at the same time, how do we choose? If all participants are honest, we could just choose arbitrarily, but if dishonest participants are present, we have to be careful: if the dishonest participant can produce lots of blocks, then choosing randomly may favour the dishonest participant over honest participants.
This then is the fundamental problem solved by blockchain technology: how do we limit the number of blocks that dishonest participants can generate? One option, known as proof-of-work and first introduced by Bitcoin, is to make block production simply costly (require a lot of time for a computer to generate). This works, but is extremely wasteful of energy; Bitcoin is consuming as much energy as a small country. The better alternative is proof-of-stake: the blockchain itself records some finite resource, and participants are allowed to produce blocks in proportion to the amount of stake they have.
Footnotes
For the purposes of this blog post I will ignore the differences between blocks and transactions. Put another way, I will assume every block contains exactly one transaction.↩︎
This number k is known as the security parameter, and is one of the most important parameters in a blockchain.↩︎
Bitcoin Mining and its Energy Footprint, Karl J. O’Dwyer and David Malone. Available online See also Bitcoin’s energy consumption is underestimated: A market dynamics approach by Alex de Vries.↩︎
This only works if the supplies someone records on the blockchain are either validated or listing supplies on the blockchain comes with a legal commitment.↩︎
Ouroboros: A Provably Secure Proof-of-Stake Blockchain Protocol. Aggelos Kiayias, Alexander Russell, Bernardo David, and Roman Oliynykov. Available online↩︎
432.000 of them, to be precise.↩︎
The proportion of slots we expect to be empty on average is known as the active slot coefficient, and is usually denoted by the variable f.↩︎
There are constraints on the value of
s. Whensis too small, doing a density comparison is not meaningful, because the probability that adversarial nodes have more than 50% stake within the window by pure luck is too large. Whensis too large, the leadership schedule within the window is no longer determined by the ledger state at the intersection point, and so the adversary can start to influence the leadership schedule. In Cardano,sis set to3k/fslots.↩︎Ouroboros Genesis: Composable Proof-of-Stake Blockchains with Dynamic Availability. Christian Badertscher, Peter Gaži, Aggelos Kiayias, Alexander Russel and Vassilis Zikas. Available online↩︎
Ouroboros Praos: An adaptively-secure, semi-synchronous proof-of-stake protocol. Bernardo David, Peter Gaži, Aggelos Kiayias and Alexander Russell. Available online↩︎
Although this means that the protocol relies on a shared notion of “time” between all participants (a wallclock), the resolution of this clock does not need to be particularly precise, and standard solutions such as NTP suffice.↩︎
