Communication Patterns in Cloud Haskell (Part 3)

Map-Reduce

In Part 1 and Part 2 of this series we described a number of ways in which we might compute the number of prime factors of a set of numbers in a distributed manner. Abstractly, these examples can be described as

a problem (computing the number of prime factors of 100 natural numbers) is split into subproblems (factorizing each number), those subproblems are solved by slave nodes, and the partial results are then combined (summing the number of factors)

This is reminiscent of Google's Map-Reduce algorithm (MapReduce: Simplified Data Processing on Large Clusters, Dean and Ghemawat, OSDI'04), with the "Map" part corresponding to the computation of partial results and the "Reduce" part corresponding to combining these results. We will explain the basic ideas behind Map-Reduce before giving a distributed implementation using work-stealing.

Local map-reduce

The exposition we give in this section is based on Google's MapReduce Programming Model -- Revisited by Ralf Laemmel (SCP 2008). The Map-Reduce algorithm transforms key-value maps; in Haskell, its type is given by

-- The type of Map-Reduce skeletons (provided by the user)
data MapReduce k1 v1 k2 v2 v3 = MapReduce {
    mrMap    :: k1 -> v1 -> [(k2, v2)]
  , mrReduce :: k2 -> [v2] -> v3
  }

-- The driver (which "executes" a Map-Reduce skeleton)
localMapReduce :: Ord k2 => MapReduce k1 v1 k2 v2 v3 -> Map k1 v1 -> Map k2 v3

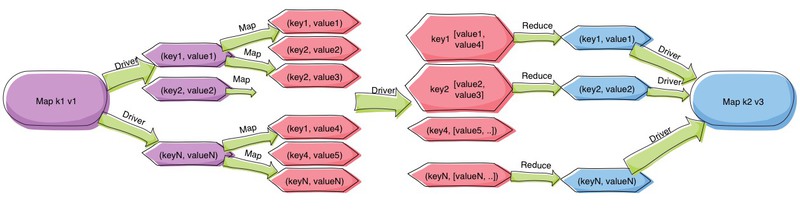
We start with a key-value map (with keys of type k1 and values of type v1). With the help of the "Map" (mrMap) part of a Map-Reduce skeleton each of these key-value pairs is turned into a list of key-value pairs (with keys of type k2 and values of type v2); note that this this list may (and typically does) contain multiple pairs with the same key. The Map-Reduce driver then collects all values for each key, and finally reduces this list of values (of type v2) to a single value (of type v3) using the "Reduce" (mrReduce) part of the skeleton.

(Colour changes in the diagram indicate type changes.)

Exercise 6: Implement localMapReduce. The types pretty much say what needs to be done.

Consider counting the number of words in a set of documents; that is, we want to transform a Map FilePath Document to a Map Word Frequency. We can do this with the following Map-Reduce skeleton:

countWords :: MapReduce FilePath Document Word Frequency Frequency
countWords = MapReduce {
    mrMap    = const (map (, 1) . words)
  , mrReduce = const sum  
  }

Distributed map-reduce

We are going to have slave nodes execute the Map part of the algorithm; we will use work-stealing to distribute the work amongst the slaves. We are not going to distribute the Reduce part of the algorithm, but do that on a single machine. For now we will give a monomorphic implementation of the distributed Map-Reduce algorithm, tailored specifically for the countWords example from the previous section. In the next post we will see how to make the implementation polymorphic.

The implementation follows the Work-Pushing example from Part 1 very closely. The slave asks for work and executes it, using the mrMap part of the Map-Reduce skeleton:

mapperProcess :: (ProcessId, ProcessId, Closure (MapReduce String String String Int Int))
              -> Process ()
mapperProcess (master, workQueue, mrClosure) = do
    us <- getSelfPid
    mr <- unClosure mrClosure
    go us mr 
  where
    go us mr = do
      -- Ask the queue for work 
      send workQueue us
  
      -- Wait for a reply; if there is work, do it and repeat; otherwise, exit
      receiveWait 
        [ match $ \(key, val) -> send master (mrMap mr key val) >> go us mr
        , match $ \()         -> return () 
        ]

remotable ['mapperProcess]

Note that the slave wants a Closure of a Map-Reduce skeleton; since the Map-Reduce skeleton itself contains functions, it is not serializable.

The master process is

distrMapReduce :: Closure (MapReduce String String String Int Int)
               -> [NodeId]
               -> Map String String
               -> Process (Map String Int)
distrMapReduce mrClosure mappers input = do
  mr     <- unClosure mrClosure
  master <- getSelfPid

  workQueue <- spawnLocal $ do
    -- Return the next bit of work to be done
    forM_ (Map.toList input) $ \(key, val) -> do 
      them <- expect
      send them (key, val)

    -- Once all the work is done tell the mappers to terminate
    replicateM_ (length mappers) $ do
      them <- expect
      send them ()

  -- Start the mappers
  forM_ mappers $ \nid -> spawn nid ($(mkClosure 'mapperProcess) (master, workQueue, mrClosure)) 

  -- Wait for the partial results
  partials <- replicateM (Map.size input) expect 

  -- We reduce on this node
  return (reducePerKey mr . groupByKey . concat $ partials)

We can now implement "distributed word counting" as

countWords_ :: () -> MapReduce FilePath Document Word Frequency Frequency
countWords_ () = countWords

remotable ['countWords_]

distrCountWords :: [NodeId] -> Map FilePath Document -> Process (Map Word Frequency)
distrCountWords = distrMapReduce ($(mkClosure 'countWords_) ())

Performance

If we use ThreadScope to look at how busy the nodes are, we find something like

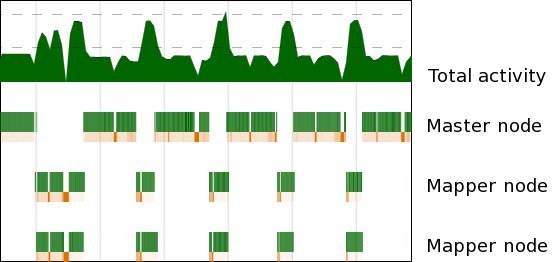
with alternating activity between the master node (which does the reduction, top) and the mapper nodes (bottom). This is unsurprising, of course; we have a distributed implementation of the Map phase but reduce locally.

Exercise 7: Change the implementation so that the reduce step happens in parallel too and confirm that the work distribution is now better.

Note: as hinted at by the ThreadScope plot above, it is possible to use ThreadScope to look at distributed applications running in multiple OS processes, including on different physical hosts. Doing so is currently a somewhat manual process. In addition to the normal step of linking the application using the -eventlog flag, and running with the flag +RTS -l -RTS, there are a few steps after the program is complete: collect the .eventlog files from each node; use the ghc-events merge command to merge all the eventlog files into one (which currently has to be done in several steps because the merge command only takes pairs of files at once) and finally use ThreadScope to view the combined eventlog.

To be continued

In the next blog post we will look at how we can make the distributed Map-Reduce skeleton polymorphic. We'll also look at k-means as an example algorithm that can be implemented using Map-Reduce. In fact for efficiency, k-means requires a "multi-shot" Map-Reduce and we'll see how Haskell and Cloud Haskell give us the flexibility we need to make this kind of extension.